工程问题属于行测试卷数量关系模块的重点题型，在近几年的公务员考试中频繁考察，从题目难度上来说，工程问题整体上难度较小，解题思路比较固定， 通过对近三年国考和省考的题目梳理，在此总结出工程问题的命题趋势，并且通过对2020年国考题目的分析，希望能对大家备考有所帮助。

　　【例1】(吉林2018-69) 甲乙两个工程队承担了精准扶贫村公路的修筑任务，先是甲工程队单独修了10天，完成了总工程的四分之一，接着乙工程队加入合作，完成剩余工程。在第14天完成到总工程的一半，则按照这种进度完成全部工程所用的天数比由甲单独完成这项工程少用的天数是：

　　A. 12天 B. 20天

　　C. 18天 D. 16天

　　【答案】C

　　【解析】第一步，本题属于工程问题给定时间型;第二步，甲单独施工10天完成总量的四分之一，所以甲完成整个工程需要40天;第三步，乙加入之后，第14天完成到工程的一半，说明甲乙合作4天可以完成总量的四分之一，甲乙合作8天可以完成总量的二分之一。所以按照这种进度完成全部工程所用的天数为14+8=22天，比甲单独施工节省40-22=18天。因此，选择C选项。

　　可以看出，吉林省考出题时题干中给定的量单一，都是只给出了时间这一类量，接下来我们看2019年国考中工程问题的考察。

　　【例2】(国家2019-69)有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天?

　　A. 不到6天 B. 6天多

　　C. 7天多 D. 超过8天

　　【答案】C

　　【解析】第一步，本题属于工程问题;第二步，设三者工作效率分别为甲、乙、丙，根据题意则有：2乙=甲+丙，3甲+3乙+7乙+7丙=7甲+7乙+7丙，得3乙=4甲，赋值甲=3，则乙=4，解得丙=5。第三步，B工程总量=10丙=10×5=50，即甲乙合作需要天)，即7天多。因此，选择C选项。

　　2019年国考中，工程问题考察了效率之间的关系，可以给效率赋值，再来看2019年吉林省考的题目。

　　【例3】(吉林2019-87)汽车厂甲、乙、丙三个机器人承担拧螺丝任务，程序设定甲先开始，3分钟后乙开始，再3分钟后丙开始。当乙工作12分钟时，所拧的螺丝数与甲拧的螺丝数相同，丙工作20分钟时，所拧的螺丝数与甲拧的螺丝数相同，则丙的工作效率是乙的( )。

　　A.1.04倍 B.0.8倍

　　C.0.9倍 D.1倍

　　【答案】A

　　【解析】第一步，本题考查工程问题，属于效率类;第二步，设三个机器人的效率分别是甲、乙、丙，甲先开始工作，3分钟后乙开始，当乙工作12分钟时，甲工作15分钟，所以12乙=15甲;当丙工作20分钟时，甲工作26分钟，所以20丙=26甲，联立可得丙=1.04乙。因此，选择A选项。

　　2019年吉林省考参照了国考中效率之间的关系进行考察，解题方法相似，题目难度比国考要小。最后来看2020年国考中工程问题的考察。

　　【例4】(国家2020-69)甲、乙两条生产线生产A和B两种产品。其中甲生产线生产A、B产品的效率分别是乙生产线的2倍和3倍。现有2种产品各X件的生产任务，企业安排甲和乙生产线合作尽快完成任务，最终甲总共生产了1.5X件产品。问乙在单位时间内生产A的件数是生产B件数的多少倍?

　　A. B.

　　C. D.

　　【答案】C

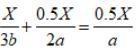
　　【解析】第一步，本题考查工程问题，效率统筹类。第二步，假设乙生产A的效率为a，则甲生产A的效率为2a，乙生产B的效率为b，甲生产B的效率为3b。两条生产线生产两种产品的效率不同，并且要求尽快完成任务，需要统筹效率，由于甲生产B产品的效率是乙的3倍，所以让甲先生产B产品，让乙生产A产品。第三步，甲生产了1.5X件，包括X件B产品和0.5X件A产品，乙生产了0.5X件A产品。所用时间相同，化简得。因此，选择C选项。

　　通过对2018和2019年国考和省考工程问题的分析，省考出题参照了国考出题的方向，2020年国考工程问题考察了多人多工程的统筹问题，需要进行相对效率对比，让效率更高的人负责他擅长的工作，可以让整体工作效率最大化。我们可以在今年备考时注意一下此类工程问题的求解，让备考更有针对性。