行测中数量关系时间短、任务重。不论是省考还是国考，平均下来几乎都是1分钟1道题，所以行测也被称作是压力型测试，相信如果给大家足够长的时间，都会取得不错的成绩，所以对于数量这个科目来说，快速选出正确答案才是取得高分的关键。那么今天华图教育就给大家介绍一种特殊的速算方法，也就是传说中的十字交叉法。

　　这种方法能帮助我们解决复杂的混合类问题，在最开始命题时，十字交叉法在溶液问题上使用频率较高，但随着难度的逐年上升，它的使用范围也进一步扩大，资料分析中也会用到十字交叉法去求解问题，因此掌握十字交叉法十分有必要。

　　先来看一种十字交叉法最简单的考察形式。

　　例：甲溶液浓度为a%，乙溶液浓度为b%，混合后得到了浓度为c%溶液，求原来甲乙溶液质量之比。

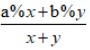
　　如果正常设未知数列方程求解的话，需要设甲溶液质量为x，乙溶液质量为y。根据溶质=溶液×浓度，甲、乙两个溶液的溶质分别可以表示为a%x、b%y。因此混合以后，新的溶质为原本两溶液中溶质的和(a%x+b%y)。同理，新的溶液质量为甲、乙两个溶液质量的和(x+y)。即新溶液的浓度可以表示为。已知求的是甲乙溶液质量之比，即x/y。所以将x/y进一步设为未知数z，令新溶液的浓度上下同时除以y，可进一步化为，即。已知新溶液浓度为c%，则，求出z=。

　　上述步骤也是对十字交叉法的原理推导过程。

　　若每次都这样推算十分浪费时间，也不利于大家在考试中快速找到正确答案，因此，十字交叉法随之产生，它就是简化了上述推理步骤，直接根据我们推导出来的关系式简单排列即可得出正确答案，方法如下：

　　混合前的比值写左边，上面一个下面一个，混合后的比值写中间，接着划十字，上减中写下面，中减下写上面，新的比值即为原公式分母的比。以这道题为例：

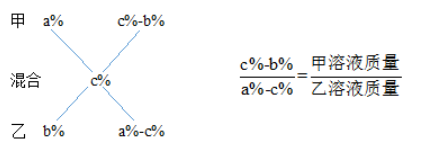
　　总结成一句话即：十字交叉的是公式的比值，得到的是分母的比。

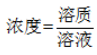
　　(例：，用浓度做十字交叉，得到的是分母(溶液)的比)

　　由于方法以及原理的特殊性，十字交叉法的应用题型也受到了一些限制，它的应用前提为：整体包含两部分，比值一高一低混成中间值。以一道真题为例。

　　【例】烧杯中装了100克浓度为10%的盐水。每次向该烧杯中加入不超过14克浓度为50%的盐水，问最少加多少次之后，烧杯中的盐水浓度能达到25%?(假设烧杯中盐水不会溢出)

　　A. 6

　　B. 5

　　C. 4

　　D. 3

　　【答案】C

　　【解析】观察发现题目间接给出了混合前的两种浓度以及混合后的溶液浓度，并且所求也与公式分母(溶液质量)有关，符合十字交叉法的前提条件，正常设未知数用公式求解也可以做，但用十字交叉法会更快速的得出答案。

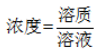
　　，交叉的是浓度，得到的是溶液质量之比。设一共加入盐水x克。

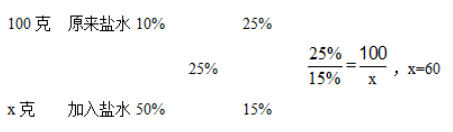
　　因此总共加入盐水共60克，由题意可知，每次加入不超过14克，则最少加入了≈4.3次，取整即5次。正确选项为C选项。

　　以上是十字交叉法在数量关系溶液问题里的应用，它也可以广泛的应用于其他含有比例关系式子的题目。例题如下：

　　【例】某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占总人数的30%，且音乐系男女生人数之比为1∶3，美术系男女生人数之比为2∶3，问音乐系和美术系的总人数之比为多少?

　　A. 5∶2

　　B. 5∶1

　　C. 3∶1

　　D. 2∶1

　　【答案】D

　　【解析】这道题虽然没有明确说明具体公式，但依据题意可以分析出来，艺术学院总人数=音乐系人数+美术系人数;男生比重=。所以可以将音乐系和美术系看成混合前的两个量，艺术学院看成是混合后的量，符合十字交叉法的前提。交叉的是比值即男生比重，得到的是分母的比，即各系总人数之比。十字交叉如下：

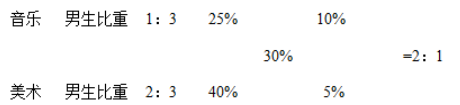
　　即音乐系总人数与美术系总人数之比为2∶1。

　　因此答案为D。

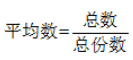
　　同样的，十字交叉法也可以广泛应用于资料分析中，、即涉及到混合平均数、混合比重以及混合增长率时，十字交叉法也可以帮助我们简化计算过程。

　　【例】2018年国家统计局组织开展了第二次全国时间利用的随机抽样调查，共调查48580人。结果显示，受访居民在一天的活动中，有酬劳动平均用时4小时24分钟。其中，男性5小时15分钟，女性3小时35分钟;城镇居民3小时59分钟，农村居民5小时1分钟;工作日4小时50分钟，休息日3小时19分钟。受访居民有酬劳动的参与率为59.0%，其中城镇居民53.1%。受访居民无酬劳动平均用时2小时42分钟。其中，女性3小时48分钟;农村居民2小时39分钟;工作日2小时34分钟。受访居民无酬劳动的参与率为70.2%，其中男性55.3%。

　　受访的男性居民约有：

　　A.2.38万人

　　B.2.43万人

　　C.2.65万人

　　D.2.91万人

　　【答案】A

　　【解析】本题所求为受访的男性居民，虽然给出了受访者的总人数，但并未给出其中男性所占的比重，所以无法直接求解。但依据题意可知受访者=男性+女性，与其有关的数据只有“有酬劳动平均用时4小时24分钟。其中，男性5小时15分钟，女性3小时35分钟”。

　　通过分析可以发现有酬劳动平均用时可以看成是男性与女性的混合平均数，故符合十字交叉法的使用条件。交叉的是比值即有酬劳动平均用时，得到的是分母(男女总人数)的比。

　　有酬劳动平均用时4小时24分钟，即264分钟;男性有酬劳动平均用时5小时15分钟，即315分钟;女性有酬劳动平均用时3小时35分钟，即215分钟。利用十字交叉可得：

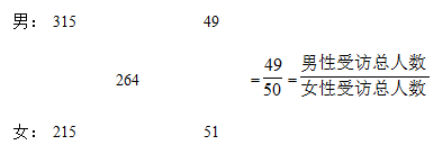
　　即男女人数之比为49：51，则男性占总人数的比重为。根据部分量=整体量×比重，则男性受访者人数约为4.86×49%≈2.38(万人)。 因此，选择A选项。

　　这就是十字交叉法的综合应用，它其实本质上是帮助我们缩短了计算的步骤，当遇到复杂的混合类比值问题时，使用十字交叉法就可以快人一步得到正确答案。也可以为其他题目争取计算时间，但也要注意灵活变通，找到题目中隐藏的比值关系，从而选出答案。