某商场为了促销，进行掷飞镖游戏。每位参与人员投掷一次，假设掷出的飞镖均扎在飞镖板上且位置完全随机，扎中中间阴影部分区域(含边线)即中奖。该商场预设中奖概率约为 60%，仅考虑中奖概率的前提下，以下四幅图形(图中的正三角形和正方形均与圆外切或内接)最适合作为飞镖板的是：

　　【解析】 ： 第一步思考 要求中奖概率约为 60%，即阴影部分的面积占飞镖板的面积约为60%，结合四个选项的图形，利用面积公式分别计算阴影部分面积占整体的比例，选择比例最接近60%的飞镖板即可。

　　第二步， 设四个选项中圆的半径均为 1，则圆的面积为π(π≈3.14)。据此可逐项分析：

　　A项，圆的内接正方形的边长为

　　= ，面积为2，阴影正方形面积与圆面积的比为 63.7%，即中奖率约为 63.7%。

　　B项，圆外切正方形的边长等于圆的直径，为2，面积为4，阴影圆面积与正方形面积的比为 ≈78.5%，即中奖率约为78.5%。

　　C项，如图1所示，圆内接三角形的边长为 ×2= ，高为 × = ，面积 为 = ， 阴影三角形 面积与圆面积的比为 ： ≈41.4% ( ≈1.732)，即中奖率约为41.4%。

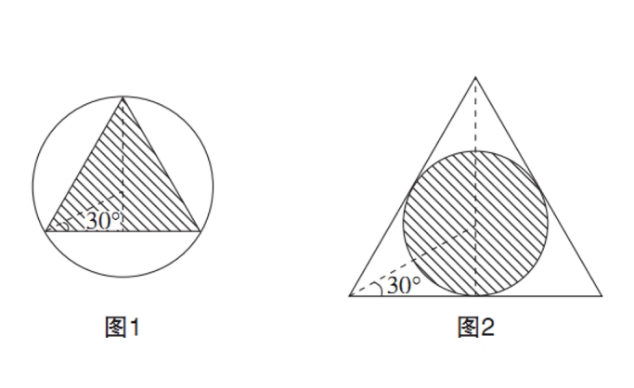
　　D项，如图2所示，圆外切三角形的边长为 ×2=2 ，高为2 × = 3 ，面积为 x2 ×3=3 ，阴影圆面积与三角形面积的比为π：3 ≈60.4%，即中奖率约为60.4%。D项中奖率最接近60%，最适合作为 飞镖板。

　　故本题选 D。