排列组合问题是数量关系中的常考题型,不管是公职考试还是事业单位考试,都作为重点备考部分。在排列组合的学习中,考生不仅需要区分排列与组合的运用,明确分类计数原理与分步计数原理,熟练掌握排列与组合的计算公式。同时,也需要学习排列组合常考特殊模型。由于考试类型的多样化,排列组合问题考点较为灵活,类型繁多,考生非常容易出错,因此,看到不同的题目类型想到对应做题方法,理解题型尤其关键。
那么排列组合有哪些常见的特殊模型呢?华图教育在此结合以下思维导图及其相关例题进行分析,以期帮助各位考生强化对于排列组合的认识。
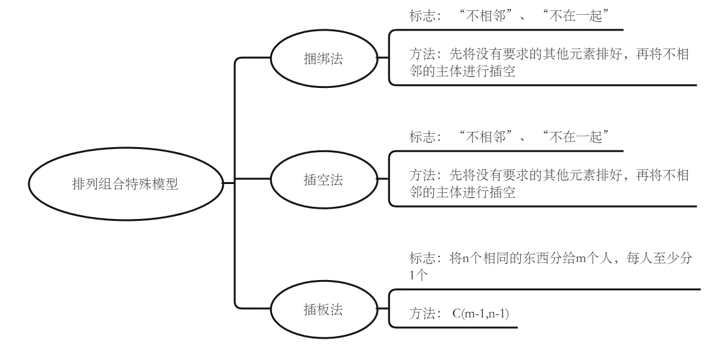
一、捆绑法
题型标志: “相邻”、“挨着”、“在一起”、“不能分开”
解题方法:先将相邻的主体捆绑在一起,再将他们视为一个整体与其他主体进行排列。
【例题】小杨、小琳等10位同学站成一横排,要求他俩必须站一块,则共有多少种排法?
A.10!
B.2!9!
C.2!8!
D.3!7!
【答案】B
【解析】 第一步,本题题型标志“站一块”,考查排列组合捆绑法。

二、插空法
题型标志: “不相邻”、 “不在一起”。
解题方法:先将没有要求的其他元素排好,再将不相邻的主体进行插空。
【例题】6棵相同的苹果树、1棵梨树和1棵橘子树种成一行,要求梨树与橘子树不相邻则有多少种排法?
A.30240
B.15120
C.42
D.21
【答案】C
【解析】 第一步,本题题型标志“不相邻”,考查排列组合插空法。

【解析】 第一步,本题题型标志“相同东西”“至少一个”,考查排列组合插板法。











