行程问题在行测中是一个常考的题型，但是很多考生认为这一类题型较难，但是大家理解了行程的相关公式，做这一类题目都会得心应手，我们先来分析一个简单的题目。

　　两个人带着宠物狗玩游戏，两人相距200米，并以相同速度1米/秒相向而行，与此同时，宠物狗以3米/秒的速度，在两人之间折返跑，当两人相距60米时，那么宠物狗总共跑的距离为?

　　A.270米 B.240米

　　C.210米 D.300米

 

　　拿到这道题，根据路程=速度×时间，很多考生在纠结小狗往返每一段路程的时间是多少，但是一段一段计算，怎样才能算出来呢?其实，小狗和两人都没有停下来，那小狗往返跑的时间就是两人行走的时间，根据两人从相距200米，相向运动至60米，共行驶200-60=140(米)，设两人运动时间为t，根据相遇公式，有140=(1+1)×t，解得t=70秒，则狗总共跑的距离为3×70=210(米)，因此，选择C选项。

　　在解题时，我们经常碰到往返型相遇问题，大家弄清楚路程、速度及时间的关系，这一类型的题目是不难的，下面再看一个此类题目：

　　甲乙两人同时沿直线跑道两端匀速相向而行，两人第一次迎面相遇时距跑道中点50米，两人到达跑道尽头时立即掉头重新出发，重新出发后两人第二次相遇，第二次两人相遇也为迎面相遇，且距跑道中点150米。则此时两人中速度较快一人比速度较慢一人多行走多少米?

　　A.150 B.400

　　C.200 D.300

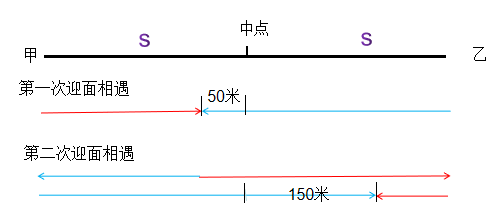
　　本题中，两人速度没有发生改变，第一次迎面相遇时两人所走路程和为一个甲到乙的全程，而第二次迎面相遇时，两人所走路程和为三个甲到乙的全程。设半程为s，快的人从出发到第一次相遇，行走s+50米，慢的人行走s-50米，从出发到第二次相遇，快的人行走(s+50)×3=3s+150米，慢的人行走(s-50)×3=3s-150米，快的比慢的多走300米，因此，选择D选项。

　　以上是直线型的相遇问题，直线型追及问题及环形相遇追及问题，大家也可以结合图形去理解核心公式，让行程问题解题时更快捷。