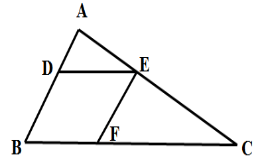
一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD，CE=2AE，CF=2BF，则三角形ADE、三角形CEF和四边形BDEF的面积之比为：( )

　　A.1:3:3 B.1:3:4 C.1:4:4 D.1:4:5 【答案】C

　　【解析】第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，由BD=2AD，CE=2AE，CF=2BF，则DE∥BC，EF∥AB，即四边形BDEF是平行四边形，可得BD=EF，DE=BF。△ADE、△EFC和△ABC相似，符合相似图形的尺寸扩大理论，

　　△EFC的边长是△ADE的2倍，面积是△ADE的22=4倍，则△ADE和△CEF的面积之比是1:4。由BD=2AD，可知AB=3AD，△ABC的边长是△ADE的3倍，面积是△ADE的32=9倍，

　　则三角形ADE、三角形CEF和四边形BDEF的面积之比为：1:4:4。

　　因此，选择C选项。