2022年7月9号省考考试在即,在最后冲刺阶段,很多小伙伴会突然焦虑,总感觉自己没准备好或者还有好多题目没看,相信小编,最后的这几天放松心情,不适合大海捞针式的学习,需要“点对点”的复习,那么什么是“点对点”呢,就是高频考点。接下来小编为大家分析数量关系与资料分析命题规律和考点预测。
数量关系
2019—2022年联考数量关系题目分布
| 题型 | 2019年 | 2020年 | 2021 | 2022.0326 | 总计 | ||||
| A 福建 | B 山西 | 725 题库 | 822 题库 | 327 题库 | 四川 | 青海 | 新疆兵团 | ||
| 基础应用题 | 7 | 7 | 4 | 12 | 2 | 2 | 4 | 38 | |
| 方程问题 | 1 | 1 | 2 | ||||||
| 工程问题 | 1 | 3 | 2 | 2 | 8 | ||||
| 几何问题 | 1 | 3 | 4 | 8 | 10 | 2 | 1 | 4 | 33 |
| 多位数问题 | 1 | 1 | |||||||
| 概率问题 | 1 | 2 | 4 | 3 | 3 | 1 | 14 | ||
| 经济利润问题 | 1 | 1 | 2 | 2 | 6 | ||||
| 容斥问题 | 1 | 1 | 2 | ||||||
| 排列组合问题 | 1 | 3 | 4 | 2 | 10 | ||||
| 余数问题 | 1 | 1 | |||||||
| 行程问题 | 1 | 2 | 2 | 2 | 1 | 8 | |||
| 约数倍数问题 | 1 | 1 | |||||||
| 溶液问题 | 1 | 1 | |||||||
| 统筹推断 | 1 | 1 | |||||||
| 函数问题 | 1 | 1 | |||||||
| 数列问题 | 3 | 1 | 1 | 1 | 1 | 7 | |||
| 最值问题 | 3 | 1 | 1 | 1 | 6 | ||||
| 时间问题 | 2 | 1 | 1 | 4 | |||||
| 其他 | 1 | 1 | 2 | ||||||
| 合计 | 10 | 10 | 27 | 26 | 43 | 10 | 10 | 10 | 116 |

2022年上半年由于疫情的原因,部分省份(四川、新疆、青海)正常举办了考试,这里小编统计了2019—2022年联考题库数量关系的题型分布。通过表格和柱状图分析可知,数量关系的考题题型创新性不是特别大,主要还是围绕基础应用题、工程问题、几何问题、概率问题、排列组合与概率问题、行程问题、数列问题、最值问题等。同时,我们发现题目类别上基础应用题和几何问题是联考考试的“宠儿”,占比较大,因此进入冲刺阶段的小伙伴,需要“点对点”的复习这两个题型。
(2022.0326青海)为了解决环卫、市政、绿化等户外作业人员吃饭难、休息难的问题。某城市设置了若干个城管驿站。如果每个城管驿站服务80人,那么有1080名户外作业人员无法得到服务;如果每个城管驿站服务100人,那么就有四个驿站空置。若要满足全部需求,则每个城管驿站至少要服务多少人?
A.93 B.94
C.95 D.96
【答案】C
【解析】第一步,本题考查基础应用题。
第二步,设驿站有x个,由题意有80x+1080=100(x-4),解得x=74,可知户外作业人员总数有70×100=7000人,每个驿站最多服务7000÷74=94.+,取整为95人。
因此,选择C选项。
(2022.0326青海)某图书馆为增加室内采光,在墙上新增一扇窗户(如下图所示)上半部分是个半圆,下半部分是个矩形。窗户用铝合金材料制作,材料总长度为27米(图中黑色线部分均为铝合金材料,铝合金宽度忽略不计,π取3)。那么该窗户的最大面积为:
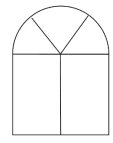
A.12平方米 B.15.75平方米
C.16.25平方米 D.18平方米
【答案】D
【解析】第一步,本题考查几何问题。

第二步,设圆的半径为r、矩形的高为h,周长为6r+πr+3h=27,解得h=9-3r,窗户的面积为πr²+2rh=1.5r²+2r(9-3r)=r(1.5r+18-6r)=4.5r(4-r),当r=4-r即r=2时,面积取到最大值,面积为4.5×2×2=18。
因此,选择D选项
资料分析
2019—2022年联考资料分析题目分布
| 题型 | 2019年 | 2020年 | 2021年 | 2022年0326 | 总计 | ||||
| A 福建 | B 山西 | 725 题库 | 822 题库 | 327 题库 | 四川 | 青海 | 新疆兵团 | ||
| 比重问题 | 2 | 2 | 12 | 4 | 7 | 2 | 2 | 9 | 40 |
| 综合分析 | 3 | 3 | 13 | 5 | 12 | 3 | 2 | 3 | 44 |
| 平均数 | 2 | 8 | 4 | 14 | |||||
| 简单计算 | 1 | 1 | 1 | 2 | 4 | 2 | 2 | 2 | 15 |
| 简单比较 | 5 | 1 | 7 | 1 | 8 | 1 | 4 | 27 | |
| 基期量与现期量 | 1 | 1 | 1 | 7 | 7 | 2 | 19 | ||
| 增长率 | 2 | 5 | 10 | 4 | 8 | 3 | 2 | 1 | 35 |
| 倍数 | 1 | 4 | 3 | 2 | 2 | 1 | 13 | ||
| 增长量 | 3 | 3 | 3 | 1 | 1 | 11 | |||
| 合计 | 15 | 15 | 59 | 29 | 55 | 15 | 10 | 20 | 218 |
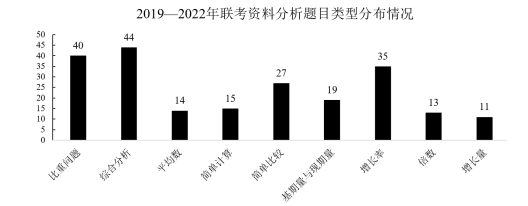
通过对近几年联考题目分析发现,资料分析的考题形式还是一篇材料5道题,其中大部分是4道小题与1道综合分析题目,题型主要是简单计算、基期量、现期量、增长量、增长率、比重、平均数与倍数,考查的也基本都是课堂所学的常见统计术语,没有特别生僻和新颖的术语与概念,因此只要大家提前系统学习、认真备考,考场上的题目可灵活应对。同时,剖析各题型考查频次,发现考查最多的是比重问题、增长率问题与简单比较,增长率问题中的增长率计算比较可以算是最近考查相对较多的知识点,因此在最后的冲刺阶段,各位小伙伴可着重复习这几个知识点。
(2022.0326青海)
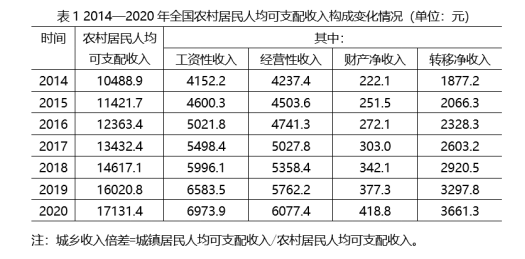
2017—2020年全国农村人均可支配收入增长最慢的年份是:
A.2017 B.2018
C.2019 D.2020
【答案】D
【解析】第一步,本题考查增长率计算比较。
第二步,定位表格材料“农村居民人均可支配收入”一列。

(2021.0327联考)截至2019年12月31日,中国共产党党员总数为9191.6万名,同比增长1.46%。在党员的性别、民族和学历上,女党员2559.9万名,少数民族党员680.3万名,大专及以上学历党员4661.5万名。在党员的入党时间上,新中国成立前入党的17.4万名,新中国成立后至党的十一届三中全会前入党的1550.9万名,党的十一届三中全会后至党的十八大前入党的6127.7万名,党的十八大以来入党的1495.6万名。在党员的职业上,工人(含工勤技能人员)644.5万名,农牧渔民2556.1万名,企事业单位、社会组织专业技术人员1440.3万名,企事业单位、社会组织管理人员1010.4万名,党政机关工作人员767.8万名,学生196.0万名,其他职业人员710.4万名,离退休人员1866.1万名。
截至2019年12月31日,资料所列8种党员职业类型中,党员人数占比不低于15%的有:
A.3类 B.4类
C.5类 D.6类
【答案】A
【解析】第一步,本题考查现期比重计算中的求比重。
第二步,定位文字材料。
第三步,根据部分量=整体量×比重,可知党员总数的15%为9191.6×15%<9200×15%=1380(万名),不低于,即大于等于,符合的有农牧渔民(2556.1万名)、企事业单位、社会组织专业技术人员(1440.3万名)和离退休人员(1866.1万名),共3类。
因此,选择A选项。










