行程问题是国考省考当中都比较常考的题型,其中多次相遇问题是考生们普遍认为难度比较大的题目,接下来我们就来介绍一下这一块比较常考的一些知识点和做题技巧。
直线型两端出发多次相遇问题常考的知识点有三个:
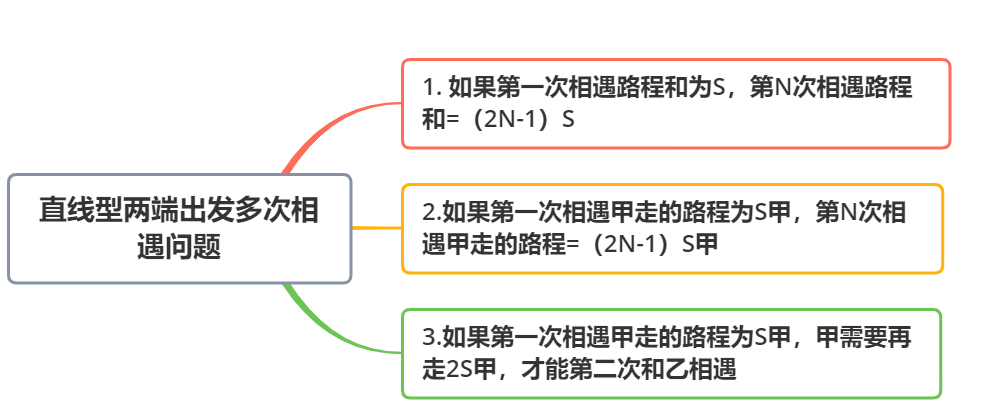
这三个重要结论,我们都可以通过画图得出:
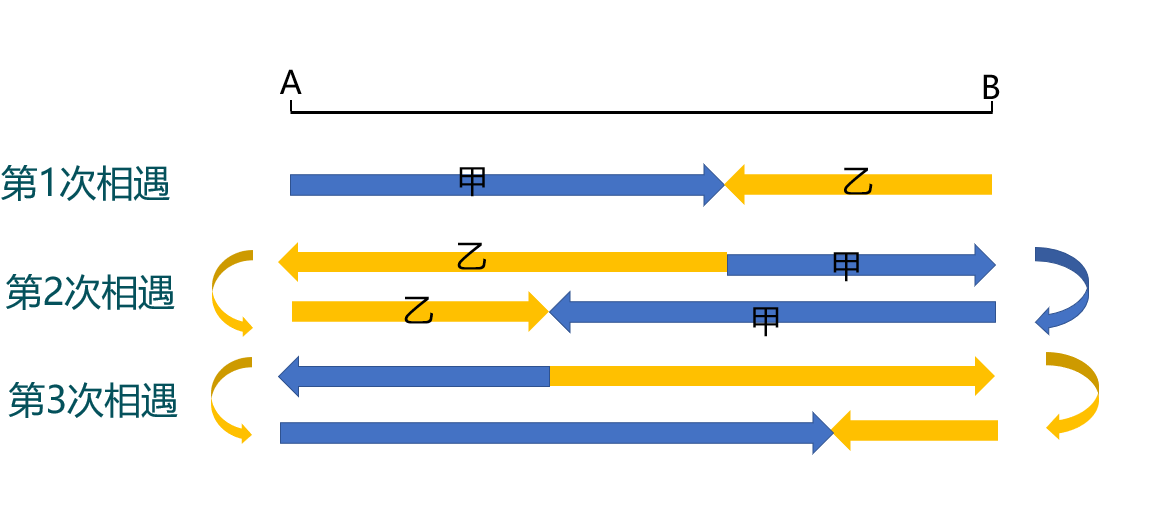
结论1:假设A、B之间的距离为S,由图可知第一次相遇的路程和为S;从第一次相遇到第二次相遇,第二次相遇到第三次相遇,以及后面每一次相遇路程和都要增加2S,所以第N次相遇路程和为(2N-1)S。结论2:甲和乙的速度和不变,路程和时间成正比,所以第N次相遇所需时间是第一次相遇所需时间的(2N-1)倍,甲的速度始终保持不变,路程和时间成正比,所以第N次相遇甲走的路程也是第一次的(2N-1)倍。结论3:假设第一次相遇甲走的路程为S甲,根据结论2第二次相遇甲走的总路程为3S甲,多以第一次相遇之后到第二次相遇之间甲走的路程是2S甲。
接下来我们看一下在真题当中如何应用这个知识点。
【例1】AB两点间有一条直线跑道,甲从A点出发,乙从B点出发,两人同时开始匀速在两点之间往返跑步。第1次迎面相遇时离A点1000米,第三次迎面相遇时离B点200米,此时甲到达B点2次,乙到达A点1次,问AB两点间跑道的长度是多少米?
A.1400B.1500
C.1600D.1700
【答案】C
【解析】
第一步,本题考查行程问题,用比例法解题。
第二步,第一次迎面相遇两人共走1个全程,第三次迎面相遇两人共走5个全程,那么两次相遇甲走过的路程之比为1∶5。设全程为s米,甲到达B点2次,则甲第三次相遇时跑的距离为3S+200米,有1000∶(3s+200)=1∶5,解得s=1600。
因此,选择C选项。
【例2】甲车从A地、乙车从B地同时出发匀速相向行驶,第一次相遇距A地100千米,两车继续前进到达对方起点后立即以原速度返回,在距离A地80千米的位置第二次相遇,则AB两地相距多少千米?
A.170B.180
C.190D.200
【答案】C
【解析】
第一步,本题考查行程问题,属于相遇追及类,用比例法解题。
第二步,设AB两地相距S千米,根据第一次相遇距A地100千米,可知甲车走了100,两人共走S;由第二次相遇距A地80千米,可知甲车从出发到第二次相遇走了2S-80,两人共走3S。
第三步,设第一次相遇时间为t1,从出发到第二次相遇时间为t2,根据速度不变,时间和路程成正比。可得,解得S=190。
因此,选择C选项。
多次相遇问题,很多时候还结合画路线图的方式来做题,画图和结论并用可以帮我们更快地解题。










